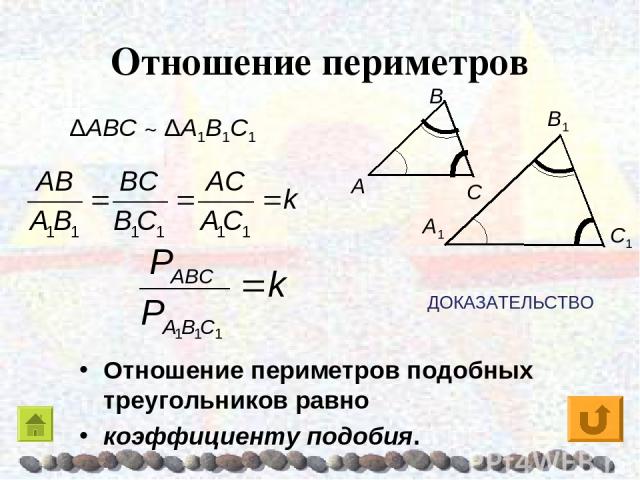
Отношение периметров подобных треугольников равно отношению
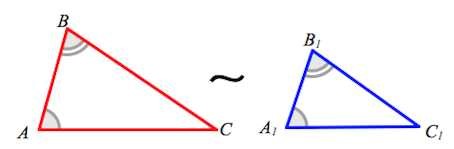
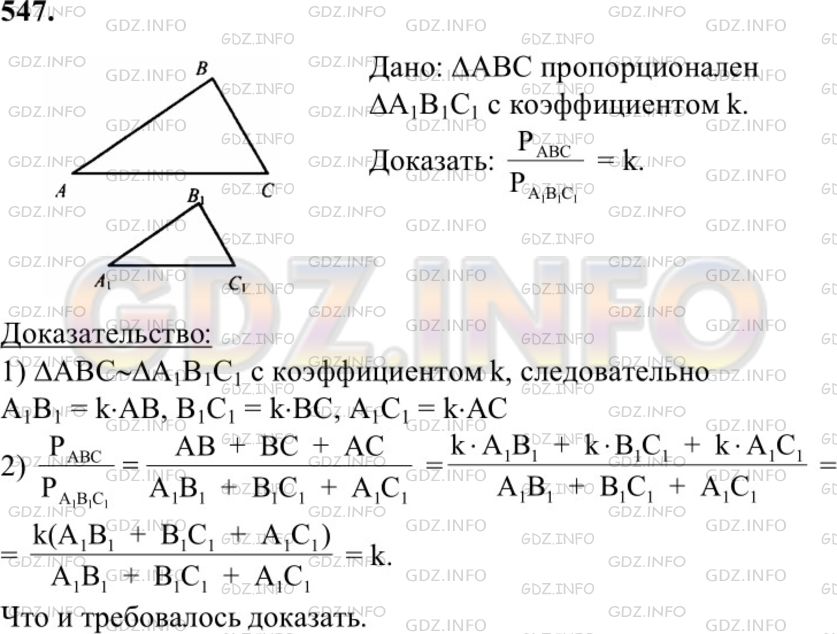
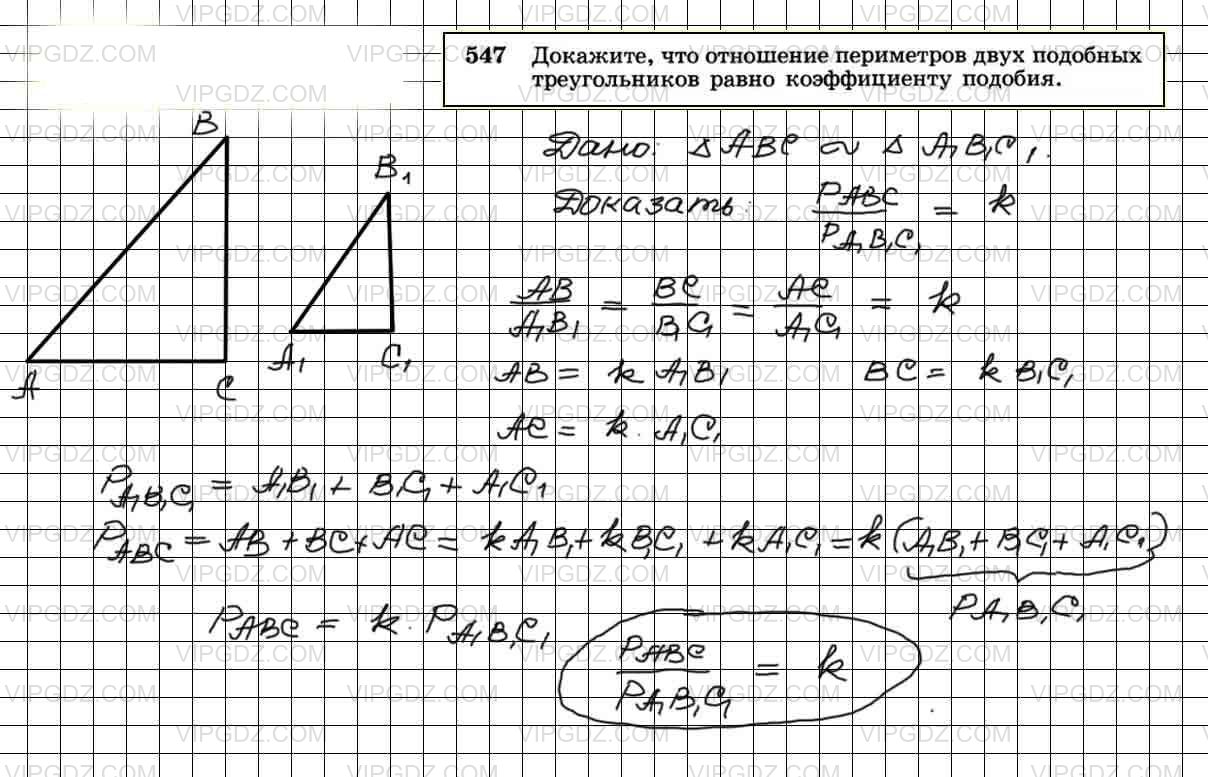
547 Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
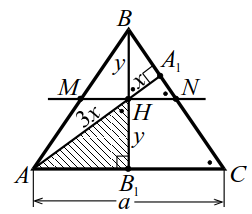
В треугольник, основание которого равно 48, а высота — 16, вписан прямоугольник с отношением сторон 5 : 9, причём большая сторона лежит на основании треугольника. Найдите стороны прямоугольника. В треугольник, у которого основание равно 30, а высота — 10, вписан прямоугольный равнобедренный треугольник так, что его гипотенуза параллельна основанию данного треугольника, а вершина прямого угла лежит на этом основании. Найдите гипотенузу. Периметр треугольника ABC равен 8. В треугольник вписана окружность и к ней проведена касательная, параллельная стороне AB.





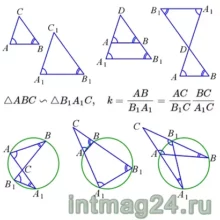
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Содержание Подобие треугольников. Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Сходственные высоты подобных треугольников относятся как коэффициент подобия.

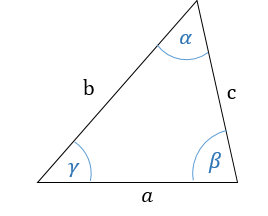
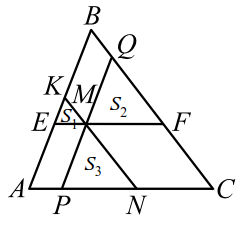






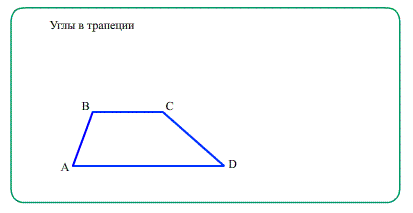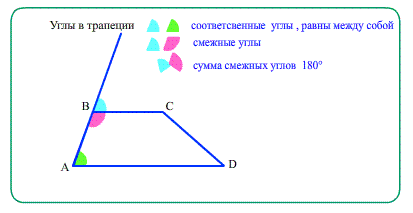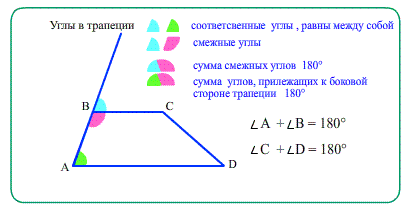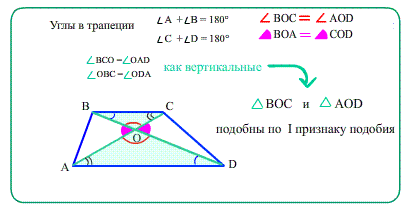
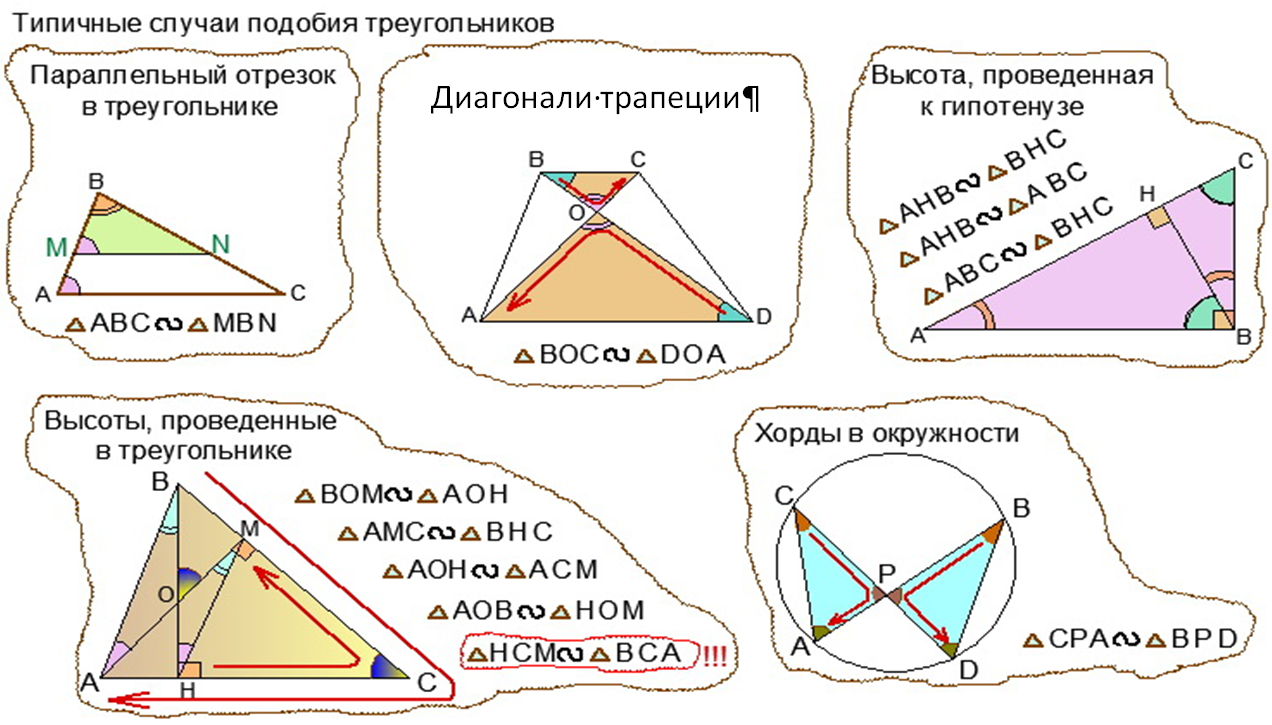
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно. Если две стороны треугольника пересекает прямая, параллельная третьей стороне рис. По первому признаку эти треугольники подобны. И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции. Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон.